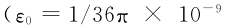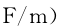【導讀】通過(guò)引入金絲鍵合線(xiàn)等效模型，建立微帶線(xiàn)旁邊增加片式電容并用金絲鍵合線(xiàn)互連后的相位補償電路物理模型。提取金絲鍵合線(xiàn)的并聯(lián)電容、串聯(lián)電感、串聯(lián)電阻等參數，計算片式電容的容值參數，推導相位補償電路物理模型的 ＡＢＣＤ 矩陣，并轉換為［Ｓ ］矩陣后，通過(guò)計算Ｓ２１參數的角度值，即可得知片式電容對傳輸微波信號相位的影響。
摘要
通過(guò)引入金絲鍵合線(xiàn)等效模型，建立微帶線(xiàn)旁邊增加片式電容并用金絲鍵合線(xiàn)互連后的相位補償電路物理模型。提取金絲鍵合線(xiàn)的并聯(lián)電容、串聯(lián)電感、串聯(lián)電阻等參數，計算片式電容的容值參數，推導相位補償電路物理模型的 ＡＢＣＤ 矩陣，并轉換為［Ｓ ］矩陣后，通過(guò)計算Ｓ２１參數的角度值，即可得知片式電容對傳輸微波信號相位的影響。同時(shí)，通過(guò)仿真試驗，驗證了該模型建立和推導的正確性。
引言
由于現在雷達系統復雜性的提高，雷達系統的回波信號經(jīng)過(guò)天線(xiàn)后，經(jīng)常需要多路接收通道同時(shí)傳送。但是通道間的固有差異，使得各路接收通道的信號輸出相位存在不一致性。為此，需要對相位進(jìn)行補償，以消除通道固有差異對相位的影響。
通常的相位補償方法是在微波電路中傳輸微波信號的微帶線(xiàn)側面增加一片覆銅層，該覆銅層作為一個(gè)片式電容與微帶線(xiàn)間用金絲鍵合線(xiàn)互連，以改變微波電路中傳輸微波信號的相位。但是該覆銅層尺寸和到微帶線(xiàn)距離對微波信號傳輸相位的影響都是由經(jīng)驗獲得，再在電路中加以調試實(shí)現。
本文通過(guò)引入金絲鍵合線(xiàn)等效電路模型，理論推導片式電容經(jīng)金絲鍵合線(xiàn)接入微帶線(xiàn)后，對整個(gè)微波電路相位的影響，并建立仿真模型進(jìn)行驗證。結果表明，理論推導與仿真結果相一致，為微波電路中相位補償調整提供了理論設計依據。
１ 金絲鍵合線(xiàn)等效模型
１．１ 等效模型
微帶線(xiàn)之間金絲鍵合線(xiàn)互連示意圖，如圖１所示。
圖１ 金絲鍵合線(xiàn)互連結構示意圖
基于微帶線(xiàn)的金絲鍵合線(xiàn)等效模型由與兩邊微帶線(xiàn)并聯(lián)的電容 Ｃ ｅ 、串聯(lián)電感 Ｌ ｂ 、串聯(lián)電阻 Ｒ ｂ等組成，如圖 ２ 所示 。
圖 ２ 金絲鍵合線(xiàn)等效模型
１．２ 模型參數計算
對自由空間中長(cháng)度為 ｌ ，直徑為 ｄ 的圓形金絲鍵合線(xiàn)，其電感 Ｌ ｂ 可表示為
式中：μ ０ 為真空磁導率
；μ ｒ為鍵合線(xiàn)的相對磁導率（對于金絲，μ ｒ ＝１ ）；δ 為鍵合線(xiàn)的趨膚深度。
；μ ｒ為鍵合線(xiàn)的相對磁導率（對于金絲，μ ｒ ＝１ ）；δ 為鍵合線(xiàn)的趨膚深度。趨膚深度 δ 的表達式為
式中：σ 為 鍵 合 線(xiàn) 的 電 導 率，對 于 金 絲， σ ＝
； ｆ 為鍵合線(xiàn)傳輸信號的頻率。
； ｆ 為鍵合線(xiàn)傳輸信號的頻率。串聯(lián)電阻 Ｒ ｂ 的計算公式為
式中：ρ 為金絲鍵合線(xiàn)的電阻率。
并聯(lián)電容 Ｃ ｅ 表示為
其中：
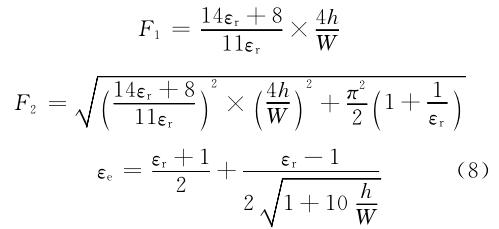
式中：ｈ 為微帶線(xiàn)基片厚度；Ｗ 為微帶線(xiàn)導帶的寬度；ε ｒ 為基片的相對介電常數。
２ 相位補償電路推導
基于微帶線(xiàn)的相位補償電路是由傳輸信號的微帶線(xiàn) 、微帶線(xiàn)旁的片式電容和金絲鍵合線(xiàn)組成，結構示意圖如圖３所示，物理模型如圖４所示。
圖 ３ 相位補償電路結構示意圖
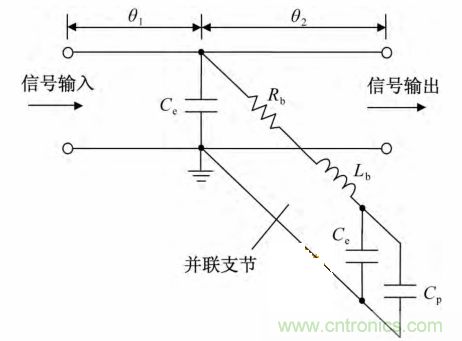
圖４ 相位補償電路物理模型
在圖４中，θ １ 是信號輸入端至金絲鍵合處的微帶線(xiàn)的電長(cháng)度，表示為
， λ ｇ 是微波信號在微帶線(xiàn)上的傳輸波長(cháng)，計算公式見(jiàn)式（６ ）。同樣，θ ２ 是金絲鍵合處至信號輸出端的微帶線(xiàn)的電長(cháng)度。 Ｃｐ 為片式電容，其電容值計算公式表示為
， λ ｇ 是微波信號在微帶線(xiàn)上的傳輸波長(cháng)，計算公式見(jiàn)式（６ ）。同樣，θ ２ 是金絲鍵合處至信號輸出端的微帶線(xiàn)的電長(cháng)度。 Ｃｐ 為片式電容，其電容值計算公式表示為
式中：ε ０ 為 真 空 介 電 常 數 
； Ａ 為片式電容單極面積。
； Ａ 為片式電容單極面積。由金絲鍵合線(xiàn)和片式電容組成的并聯(lián)支節，在電路中作為并聯(lián)導納，表示為
其中：
因此，圖４中從信號輸入至信號輸出級聯(lián)網(wǎng)絡(luò )的歸一化 ＡＢＣＤ矩陣如下表示 ：
式中：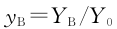
， Ｙ ０ 為微帶線(xiàn)的特性導納。
， Ｙ ０ 為微帶線(xiàn)的特性導納。
根據矩陣［ ａ ］至矩陣［ Ｓ ］的轉換公式（１２）將式（１１）轉化為矩陣［ Ｓ ］，計算參數 Ｓ２１的角度值為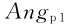
，即為引入片式電容后微波信號從輸入端傳至輸出端的相位延遲值。
，即為引入片式電容后微波信號從輸入端傳至輸出端的相位延遲值。在不引入片式電容的情況下，計算微波信號在相同微帶線(xiàn)上傳輸的相位延遲值為
因此，計算
即為片式電容引入的相位補償值。
即為片式電容引入的相位補償值。同理，當一個(gè)片式電容不足以對所需相位進(jìn)行補償時(shí)，可以引入兩個(gè)片式電容，其物理模型如圖５所示。
圖 ５ 兩個(gè)片式電容相位補償模型
計算其歸一化 ＡＢＣＤ矩陣為
根據轉換式（１２），將矩陣［ａＴ２ ］轉換為矩陣［Ｓ］，得出參數 Ｓ２１ 的角度值，與微帶線(xiàn)本身的相位延遲作比較，算出相位補償值。
３ 理論推導與仿真試驗比對
通過(guò)建立仿真模型對理論推導進(jìn)行驗證，仿真模型示意如圖６所示。圖中，微帶線(xiàn)基片厚度ｈ＝０.１２７ｍｍ ；相對介電常數 ε ｒ＝２.２ ；特性阻抗Ｚ０ ＝５０Ω ；鍵合金絲長(cháng)度 ｌ＝８００ μ ｍ ；直徑 ｄ＝２５ μ ｍ ；片式電容尺寸為０.３ｍｍ×０.３ｍｍ 。若工作頻率為２０ＧＨｚ ，微帶線(xiàn)總長(cháng)度為３倍 λ／４ ，兩個(gè)片式電容間隔 λ ／４ 。
圖６ 相位補償仿真模型示意圖
由理論推導和仿真試驗得出的輸入端與輸出端相位延遲比較如表１所示。從中看出，插入１個(gè)或２個(gè)片式電容時(shí)，理論推導算得的相位補償分別為６.５° 、 １３.１° ，仿真試驗得出相位補償分別為６.８° 、 １４.０° ，理論推導的數據與仿真試驗的數據一致性很好。
表 １ 理論推導和仿真試驗數據比對
通過(guò)進(jìn)一步的分析計算，可以得出以下結論：多個(gè)片式電容間隔無(wú)需滿(mǎn)足１／４波長(cháng)要求；片式電容位置不能離微帶線(xiàn)太遠，否則過(guò)長(cháng)的金絲鍵合線(xiàn)會(huì )增加鏈路的插損，特別在工作頻率提高后。
４ 結論
本文通過(guò)引入金絲鍵合線(xiàn)等效模型，建立由微帶線(xiàn)旁邊增加片式電容并用金絲鍵合線(xiàn)互連后的物理模型，將該模型轉換為矩陣［Ｓ］后，計算增加片式電容對傳輸微波信號的相位影響。同時(shí)，通過(guò)仿真試驗，驗證了該模型建立和推導的正確性。因為可以方便地在微帶線(xiàn)旁邊增加片式電容，所以本文的分析對微波鏈路中靈活的相位補償具有參考作用。
免責聲明：本文為轉載文章，轉載此文目的在于傳遞更多信息，版權歸原作者所有。本文所用視頻、圖片、文字如涉及作品版權問(wèn)題，請電話(huà)或者郵箱聯(lián)系小編進(jìn)行侵刪。
